doi.org/10.15178/va.2017.140.45-54

INVESTIGACIÓN

USO DE LA PERMUTACIÓN CON REPETICIÓN COMO ENSEÑANZA DE EXPERIMENTOS BINOMIALES

USE OF REPETITIVE PERMUTATION AS BINOMIAL EXPERIMENT TEACHING

USO DA PERMUTAÇÃO COM REPETIÇÃO COMO ENSINAMENTO DE EXPERIMENTOS BINOMIALES

Antonio José Boada¹ Licenciado en Educación mención Física y Matemáticas. Especialista en Estadística Computacional. Magister en Finanzas. Autor y ponente en más de 30 congresos internacionales arbitrados e indexados. Autor de más de 10 artículos en revistas científicas arbitradas e indexadas. Profesional íntegro, con experiencia en áreas Financieras, Marketing, Demand Planning & Supply Chain. Especialista en Empresas con Estilo de Venta Directa. Manejo de Herramientas virtuales de enseñanza Moodle & Sakai. Clasificación Educativa, Valoración e Ingreso a Nivel Superior. Enseñanza Virtual a Distancia y uso de las TIC’s. Venezolano, emigrado a Colombia. https://scholar.google.es/citations?user=Zv0EdDoAAAAJ&hl=es

¹CEIPA Business School. Escuela de Administración. Medellín. Colombia

RESUMEN

Mediante este artículo, se expone al lector dos (2) formas de enseñanza para los Experimentos Bernoulli “Éxito – Fracaso”, consolidadas en la Distribución Probabilística Binomial y explicados desde dos (2) concepciones de conteo: con repetición y sin repetición. La Distribución Binomial, concebida como una distribución probabilística discreta de éxitos y fracasos (experimentos de Bernoulli), presenta su característica más importante en el conteo de escenarios, determinado por una expresión que diversos autores han determinado como número combinatorio sin repetición, cuando es factible exponerlo también como una permutación con repetición en dos (2) escenarios, de éxito y fracaso. La coincidencia numérica entre el uso de la permutación con repetición y el número combinatorio sin repetición, resulta interesante de analizar, propiciando argumentos explicativos que pudieran apoyar al docente para dos contextos de enseñanza – aprendizaje para la Distribución Binomial; por un lado, el método tradicional de número combinatorio sin repetición, en una distribución probabilística con sucesos independientes; y por el otro mediante un método de conteo análogo a la Distribución Probabilística Multinomial y que expone un proceso de enlace entre los ensayos independientes Bernoulli, mediante el conteo de los eventos del espacio muestral mediante una permutación con repetición, particularizado para el caso de 2 escenarios complementarios (éxito y fracaso). Es por ello, que todo educador, debe conocer y manejar ambos contextos de enseñanza – aprendizaje para la Distribución Binomial, a fin de potenciar las estrategias pedagógicas necesarias para contemplar la teoría combinatoria con repetición o con reemplazo, mediante la opción de permutaciones con repetición en caso de ser requerida.

PALABRAS CLAVE: Permutación, Experimentos de Bernoulli, Distribución Probabilística Binomial, Teoría Combinatoria, Permutación con Repetición

ABSTRACT

This article presents the reader two (2) ways of education for Experiments Bernoulli “Success - Failure” consolidated in the Probabilistic Binomial Distribution and explained from two (2) counting concepts: with repetition and without repetition.
Binomial Distribution, conceived as a discrete probabilistic distribution of successes and failures (experiments of Bernoulli), presents its most important characteristic in the counting of scenarios, determined by an expression determined by several authors as combinatorial number without repetition, when it is feasible to present it also as a permutation with repetition in two (2) scenarios, success and failure. It is interesting to analyze the numerical coincidence between the use of permutation with repetition and the combinatorial number without repetition, promoting explanatory arguments to support teachers for two contexts of teaching - learning for the binomial distribution; on the one hand, the traditional method of combinatorial number without repetition, in a probabilistic distribution with independent events and, on the other hand, by way of a method of analogous counting to the Probabilistic Multinomial Distribution that presents a binding process between independent Bernoulli trials, by counting the events of the sample space through permutation with repetition, particularized for the case of 2 complementary scenarios (success and failure). This is why every educator should know and manage both contexts of teaching - learning for Binomial Distribution, in order to enhance the teaching strategies necessary to contemplate the combinatorial theory with repetition or with replacement, with the option of permutations with repetition if required.

KEYWORDS: Permutation, Bernoulli Experiments, Binomial Probabilistic Distribution, Combinatorial Theory, Permutation with Repetition

RESUMO

Mediante este artigo, se expõe ao leitor duas formas de ensinamento para os Experimentos Bernoulli ¨Exito-Fracasso¨, consolidados na Distribuição Probabilista Binomial e explicados desde duas concepções de contagem: com repetição e sem repetição. A distribuição Binomial concebida como uma distribuição probabilística discreta de êxitos e fracassos (experimentos de Bernoulli) apresenta sua característica mais importante na contagem de cenários, usado por uma expressão que diversos autores determinaram como número combinatório sem repetição quando é viável expor também como uma permutação com repetição em dois cenários, de êxito e fracasso. A coincidência numérica entre o uso da permutação com repetição e o número combinatório sem repetição, resulta interessante de analisar, propiciando argumentos explicativos que puderam apoiar ao docente para dois contextos de ensinamento – aprendizagem para a Distribuição Binomial; por um lado, o método tradicional de números combinatórios sem repetição, em uma distribuição probabilística com sucessos independentes; e por outro lado, mediante um método de contagem análogo a Distribuição Probabilística Multinomial e que expõe um processo de enlace entre os ensaios independentes Bernoulli, mediante a contagem dos eventos do espaço de amostras mediante uma permutação com repetição, particularizado para o caso de dois cenários complementários (êxito e fracasso).
É por isso que todo educador deve conhecer e manejar ambos contextos de ensinamento – aprendizagem para a Distribuição Binomial, afim de potenciar as estratégias pedagógicas necessárias para contemplar a teoria combinatória com repetição ou com substituição, mediante opção de permutações com repetições em caso de ser requerida.

PALAVRAS CHAVE: Permutação, Experimentos de Bernoulli, Distribuição Probabilística Binomial, Teoria Combinatória, Permutação com Repetição

Recibido: 14/03/2017
Aceptado: 08/05/2017
Publicado: 15/09/2017

Correspondencia: Antonio José Boada. antonio_boada@virtual.ceipa.edu.co

1. INTRODUCCIÓN

En cualquier experimento aleatorio, los resultados se presentan al azar; así, a éste se le denomina variable aleatoria. Cada valor de la variable aleatoria se relaciona con una probabilidad que indica la posibilidad de un resultado determinado. (Lind, 2012). En este sentido, la variable aleatoria expone la cantidad que resulta de un experimento que, por azar, puede adoptar diferentes valores.
La distribución de probabilidad binomial es una distribución de probabilidad discreta que se presenta con mucha frecuencia. Una de sus características consiste en que sólo hay dos posibles resultados en un determinado ensayo del experimento. Los resultados son mutuamente excluyentes, lo cual significa que la respuesta a una pregunta de cierto o falso no puede ser al mismo tiempo cierta o falsa. (Lind, 2012). Así mismo, una característica de la distribución binomial consiste en que cada ensayo es independiente de cualquier otro. Que sean independientes significa que no existen patrones en los ensayos. El resultado de un ensayo particular no influye en el resultado de otro ensayo.
La Distribución Binomial presenta la valoración de una serie de ensayos en experimentos de Bernoulli, cuantificados mediante un número combinatorio sin repetición, aspecto que puede dificultar en el proceso de enseñanza, ya que los experimentos de Bernoulli se calculan en escenarios independientes, donde si existe repetición.
Bajo la concepción de la Distribución Binomial, (Shao, 1967 p. 274), se expone una deducción de la fórmula mediante un ejemplo de extraer dos (2) bolas blancas en tres (3) extracciones con reemplazo, bajo un universo de una bolsa con cinco (5) bolas, donde una es blanca y cuatro (4) son negras. En este aspecto, Shao deduce correctamente la probabilidad de “éxito”, correspondiente a 1/5, y la de fracaso 4/5; esto con la finalidad posterior de establecer el escenario en donde se extraigan finalmente 2 bolas blancas en 3 extracciones, lo que daría como resultado (1/5)(1/5)(4/5), bajo la combinación de resultados BBN, BNB, NBB (es decir 3 opciones en donde es posible obtener 2 bolas blancas y una negra). Sin embargo, Shao define el cálculo de estas 3 opciones como un número combinatorio sin repetición nCk, en donde “n” expone número de extracciones (3) y “k” el número de ocurrencias del evento “bola blanca” (2). Aspecto, que pedagógicamente puede generar problemas interpretativos en el proceso de enseñanza, ya que el número de ocurrencias “k” no es un elemento sin repetición, sino más bien al contrario, puede ser una permutación con aspectos (3 extracciones) que se repiten (2 bolas blancas), lo que expondría el uso de una permutación con repetición.
En este sentido, tomando el ejemplo anterior, puede resultar complicado para el docente considerar la cuantificación de casos mediante un número combinatorio sin repetición, cuando puede fácilmente representarse como una permutación con repetición, particularizada a dos (2) escenarios: Éxito y Fracaso.
La teoría combinatoria presenta dos (2) concepciones: con repetición y sin repetición. Como su nombre lo dice, con repetición significa que los términos pueden volver a aparecer o cuando el número de eventos es contante, es decir, no varía el universo con la extracción (Díaz, 2013), como por ejemplo eventos independientes binomiales: 3 caras y 4 sellos cuando se lanza 7 veces una moneda.
Diversos autores como Walpole, 1998 y Webster, 2003, intentan explicar pedagógicamente esta tergiversación argumentando que el número combinatorio sin repetición nCk corresponde al conteo de “n” experimentos de Bernoulli, para seleccionar “k” casos en donde hay “k” éxitos, como si fuera un caso de combinatoria sin repetición, pero resulta que bajo esta concepción, se debería presentar una disminución del espacio muestral original (universo de “n” experimentos Bernoulli), aspecto que no sucede, ya que siempre fueron “n” experimentos de Bernoulli, y siempre fueron “k” éxitos, lo único que en realidad ha cambiado es el orden en que los éxitos son valorados en los distintos ensayos de Bernoulli.
Una Distribución Binomial, siempre buscará contar los experimentos independientes de Bernoulli, y este artículo expone una propuesta de realizarla mediante el uso de permutaciones con repetición, que pueden modelar el número de anagramas de los casos independientes EEE…EFFF…F, en donde se tienen “k” experimentos de E (éxito) y que tiene “n-k” experimentos de F (Fracaso).

2. OBJETIVO

Comprobar matemáticamente que la expresión de conteo utilizado por una Distribución Probabilística Binomial puede ser representada por la permutación con repetición de “n” experimentos de Bernoullli.
Mediante este objetivo, se busca potenciar el uso de la permutación con repetición, y exponer al docente una nueva opción de enseñanza de la distribución binomial desde la perspectiva de “n” experimentos independientes de Bernoulli.

3. METODOLOGÍA

3.1. Marco de referencia. Número combinatorio sin repetición

El número combinatorio, o la combinación sin repetición, expresa el conteo de maneras de elegir “k” elementos dentro de los “n” casos posibles, sin considerar el orden de selección.

Las combinaciones son todos los subconjuntos de “k” elementos que se pueden formar de entre un conjunto de “n” objetos, y en donde una combinación con los mismos elementos no es otra combinación, sino que es la misma, aunque los elementos se encuentren en diferente orden. (Díaz, 2013).
En el caso de un número combinatorio sin repetición, la presencia de eventos dependientes es fundamental, ya que el universo de elementos se modifica en función a la selección de elementos “exitosos” que se van tomando en consideración. Cómo su nombre lo dice, debe utilizarse en elementos de conteo dependientes (sin repetición), y no en escenarios de conteo independientes o con repetición (tal como es el caso de la distribución Binomial).

3.2. Permutación con repetición

La permutación con repetición expresa una forma de cuantificar las posibles posiciones de los eventos, excluyendo aquellos que tengas iguales características.

Donde “n” corresponde al número total de casos, mientras que los “ki” representan las clasificaciones realizadas según las características a segmentar (pudiendo ser éxito y fracaso para el caso binomial); por ende, Σki = n. (Meyer, 1999)

Es necesario, establecer siempre la diferenciación entre la teoría combinatoria con repetición (independiente o con reemplazo), vs la teoría combinatoria sin repetición (dependiente o sin reemplazo). Algunos autores, como Anderson, 2016 expresan un único enfoque a la teoría combinatoria sin repetición (sin colocar la salvedad de la existencia de otra forma de conteo). Así mismo, autores como Walpole, (1998, p. 121) expone la permutación con repetición, como un número combinatorio de diversos “grupos”.

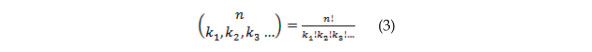
Sin embargo, independientemente de los expuestos por diversos autores, la teoría combinatoria con repetición plantea un conjunto de herramientas que pueden ser utilizadas y aplicadas en todos aquellos conjuntos en donde sea permitido repetir elementos.
Bajo esta concepción, la permutación con repetición expone una forma de conteo excelente para escenarios independientes, en donde el universo no varía con la selección de escenarios; por ende puede ser aplicado directamente al conteo de eventos “número de eventos exitosos vs número de eventos no exitosos”, convirtiéndose en una herramienta ideal para la enseñanza de las distribuciones probabilísticas de experimentos independientes, como la Distribución Binomial.
Mediante permutación con repetición (número que veces que se repiten los casos de éxito y el número de veces que se repiten los casos de fracaso), es posible el uso cónsono y sinérgico de una misma teoría de enseñanza (con repetición) en eventos de Bernoulli, los cuales son claramente independientes en su naturaleza.

3.3. Similitud entre la Permutación con Repetición y el Número Combinatorio sin Repetición

Cuando se poseen dos (2) características a segmentar, como éxito y fracaso, la fórmula de permutación con repetición coincide con la fórmula de número combinatorio sin repetición. Recordando que

por ende, si

entonces,

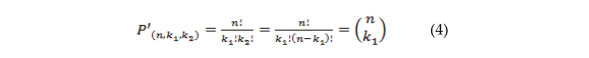
Por este motivo, el conteo de los experimentos de Bernoulli, que es un problema sencillo de permutación con repetición (caso particular para 2 escenarios), se ha tergiversado como un número combinatorio sin repetición, bajo escasos argumentos pedagógicos para explicar su origen. (Boada, 2001).
Algunos autores, explican esta tergiversación argumentando que corresponde al conteo de “n” experimentos de Bernoulli, para seleccionar “k” casos en donde hay “k” éxitos (Díaz, 2013, Pag. 152), como si fuera un caso de combinatoria sin repetición, pero resulta que bajo esta concepción no hay ninguna disminución ni alteración del universo ni del espacio muestral original, ya que siempre fueron “n” experimentos de Bernoulli, y siempre fueron “k” éxitos, lo único que en realidad ha cambiado es el orden en que los éxitos son valorados en los distintos ensayos de Bernoulli. Esta explicación resulta incongruente, en una distribución probabilística cuyo bastión principal es la independencia de los experimentos de Bernoulli, y en donde su espacio muestral no debe presentar alteraciones.
Una Distribución Binomial, buscará siempre cuantificar la cantidad de experimentos Bernoulli, que pueden modelarse según el número de anagramas de los “n” casos independientes EEE…EFFF…F, en donde se definan “k” experimentos de E (éxito) y que tiene “n-k” experimentos de F (Fracaso).

4. DISCUSIÓN

4.1. Distribución Binomial, análisis desde 2 perspectivas

La Distribución Binomial es una distribución de probabilidad discreta que cuantifica el número de éxitos en una secuencia de “n” ensayos de Bernoulli independientes entre sí, con una probabilidad fija “p” de ocurrencia del éxito. (Webster, 2003)
Si consideramos un experimento, y sea A un suceso aleatorio con el experimento, podemos suponer que P (A) = p, y por lo tanto (por ser experimento Bernoulli) P (A) = 1 – p. Luego, considerando “n” repeticiones independientes del experimento, generamos el espacio muestral en todas las sucesiones posibles según A y A ocurran.
Así mismo, se supone que P (A) = p es constante para todas las repeticiones (característica de independencia entre eventos). Dada estas premisas, podemos definir una variable aleatoria X = Número de veces que ocurrió el suceso A, dados los parámetros “n” y “p”. (Meyer, 1999)
Bajo esta definición, la variable aleatoria X corresponde a una variable Binomial, con los parámetros “n” y “p”, y cuyos valores son 0, 1, 2, 3, …, n. Donde las repeticiones individuales e independientes de los experimentos se denominan ensayos de Bernoulli.

En este sentido, la expresión

cuantifica la cantidad de ensayos de Bernoulli en donde se pueden combinar los Éxitos (p) y los Fracasos (1 – p) en “n” opciones posibles. Esta expresión resulta en consonancia con la definición y uso de la permutación con repetición previamente explicada, y no como un número combinatorio sin repetición, que usualmente se coloca en los libros de textos estadísticos.
Analicemos a continuación un sencillo ejemplo del lanzamiento de “n” dados.

4.2. Distribución Multinomial

Así mismo, cuando se analiza la distribución Multinomial, en ésta aparece en efecto cuantificada la presencia de casos mediante la Permutación con Repetición generalizada para la diversidad de casos.
Se considera un experimento, su espacio muestral S, y una partición de S en “k” sucesos mutuamente excluyentes A1, A2, A3, …, Ak, y consideramos “n” repeticiones independientes de los experimentos. Sea pi = P(Ai) y supóngase que pi permanece constante durante todas las repeticiones de cada suceso, entonces

y se define el siguiente teorema, que da vida a la Distribución Multinomial.

Si Xi, i = 1, 2, 3, …, k están definidas bajo los preceptos anteriores, entonces

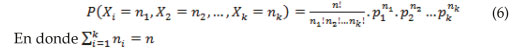
Es de hacer notar que Xi, no son variables independientes, ya que la suma es igual al número total de datos. (Meyer, 1999).

5. CONCLUSIONES

Mediante este artículo, podemos evidenciar una nueva perspectiva de enseñanza para la Distribución de Probabilidad Discreta Binomial, en función a una serie de ensayos independientes Bernoulli, cuantificados mediante una teoría de conteo con repetición, a través del uso de la permutación con repetición, particularizado para el caso de 2 escenarios complementarios (éxito y fracaso).
A nivel de enseñanza de la Distribución Binomial, esta nueva forma, establece una sinergia con la concepción de independencia de los experimentos de Bernoulli, ya que esta nueva perspectiva expone una teoría combinatoria de conteo para eventos independientes (con repetición o con reemplazo), mediante la opción de permutaciones con repetición.
Con el pasar de los años, el uso, manejo y explicación de la teoría combinatoria con repetición ha sido relegada en la enseñanza de la estadística, brindando mayor protagonismo a la teoría combinatoria sin repetición. Esta ausencia, ha permitido potenciar la enseñanza de la distribución binomial bajo una sola concepción, sin percatarse que existe otra manera de explicar no sólo la Distribución Binomial, sino inclusive la Distribución Multinomial, mediante la misma teoría de conteo combinatorio con repetición.
Mediante este artículo, el lector podrá visualizar la presencia de dos (2) formas de enseñanza para el conteo de escenarios en una Distribución Probabilística Binomial:
1. La explicación tradicional mediante el uso de un número combinatorio sin repetición nCk corresponde al conteo de “n” experimentos de Bernoulli, para seleccionar “k” casos en donde hay “k” éxitos.
2. Explicación novedosa mediante el uso de una permutación con repetición, en donde se muestra invariante el espacio muestral original (universo de “n” experimentos Bernoulli) y “k” éxitos, cambiando únicamente el orden en que los éxitos son valorados en los distintos ensayos de Bernoulli.

REFERENCIAS

1. Anderson DR, Dennis JS, Thomas AW (2016). Estadística para Negocios y Economía. Londres: Cengage Learning.
2. Boada A (2001). Uso de la Permutación con Repetición, como Herramienta para la Enseñanza de la Probabilidad. Matanzas, Cuba: COMAT’01, Universidad de Matanzas.
3. Díaz-Mata A (2013). Estadística aplicada a la administración y la economía. McGraw-Hill Interamericana.
4. Douglas-Lind A (2012). Estadística aplicada a los negocios y la economía. McGraw-Hill Interamericana.
5. Meyer P (1999). Probabilidad y Aplicaciones Estadísticas. Addisson: Wesley Iberoamericana.
6. Shao-Stephen P (1967). Estadística para Economistas y Administradores de Empresas. México: Herrero Hermanos, Sucs.
7. Walpole R, Raymond M, Sharon M (1999). Probabilidad y estadística para ingenieros. Pearson Educación.
8. Webster-Allen L (2003). Estadística aplicada a los negocios y la economía. Bogotá: Mc Graw Hill.